[12] - Space and transforms - 2

이번에는 이차원 공간이 아닌 삼차원 공간에서 물체들을 다루어 보도록 합니다.

Scaling

Scaling은 이차원 공간과 극적으로 대비되는 부분은 없습니다. 단순히 요소가 하나 더 증가했을 뿐입니다.

이차원 공간에서는 z의 모습을 볼 수 없었습니다

여기서 scaling factor가 서로 같다면 이 scaling은 "uniform scaling"이라고 부릅니다. 그것이 아니라면 "non-uniform"이라고 합니다. 이 factor가 1보다 크다면 물체는 확대가 될 것이고 0보다 크고 1보다 작다면 물체는 줄어들 것입니다.

Rotation

이차원 공간에서 회전을 하기 위해서는 점을 기준으로 회전했습니다. 하지만 삼차원 공간에서는 점이 아니라 축을 두고 회전을 합니다. 따라서, 삼차원 공간 상의 회전은 회전하는 축을 기준으로 각기 다른 회전의 양상을 보입니다. 

z축 말고 다른 축으로도 회전할 수 있습니다

 

z축 회전의 경우는 이차원 공간 상에서 원점을 기준으로 한 회전과 크게 다르지 않습니다

이번엔 x축을 기준으로 회전한다고 가정해봅니다. 먼저, 양의 방향 회전은 무조건 anti-clockwise가 기본이라는 점을 염두에 두고 진행합니다. 따라서 x축을 기준으로 회전하면 y축의 점들이 z축을 향해 이동할 것입니다.

 

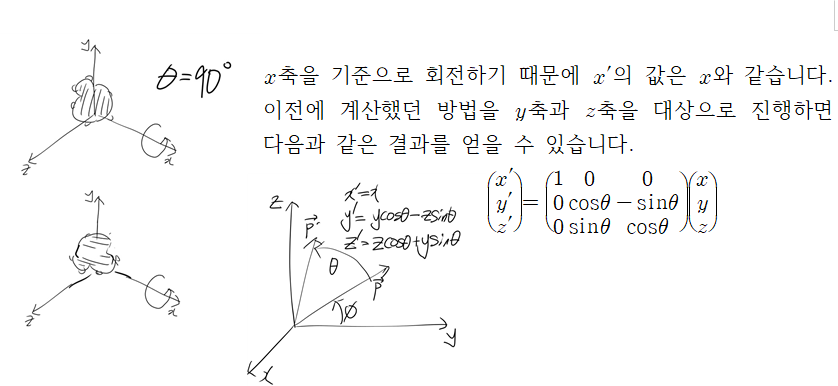
y축 회전도 기본 개념이 완전히 같습니다. 어려운 것이 하나도 없으니 넘어갑니다.

Translation

translation은 벡터의 합의 형태지만 곱의 형태로 만들 수 있었습니다. 삼차원 공간에서도 똑같은 일을 합니다. 3x3 행렬을 4x4로 만들어 진행합니다. 이차원 공간 상에서 Cartesian coordinates를 Homogeneouse coordinates로 바꾸어 사용했던 방법이 삼차원 공간 상에서도 똑같이 적용됩니다.

 

World Transform

지금까지는 Object space를 설명한 것에 불과합니다. 지금까지 어떤 물체가 회전한다고 하면 모든 좌표가 그 물체를 기준으로 설명되어 있는 세상이었습니다. 즉, '원점'은 무조건 해당 물체가 중심이었습니다. 이러한 각각의 Object들을 하나의 공간에 몰아 놓은 Scene 또는 Space를 World Space라고 합니다. Object space 상의 Vertex들을 World space 상의 Vertex 좌표로 변환해 주는 Transform이 바로 World Transform입니다. 그래서 World transform은 단 하나만 존재하는 것이 아니고 다양하게 존재할 수 있습니다. 그렇지 않으면 world transform만 진행했을 때 모든 물체가 한 지점에 겹쳐버리는 사태가 일어날 테니까요.

3D Affine transforms

행렬의 계산은 교환 법칙이 성립하지 않는다고 했습니다. 그럼에도 불구하고 [L|t]나 [R|t]로 표현이 될 경우엔 서로 교환을 해도 같은 이동 결과를 얻을 수 있었습니다. 이런 성질은 삼차원 공간에서도 유효합니다.

Rotation and Object space Basis

Object space 상의 어떤 물체를 회전한다는 것은 단순히 vertex를 이동하는 것에서 그치는 것이 아닙니다. World space로 개념이 확장되면서 object가 중심으로 삼는 각 축이 함께 회전했다고 보는 편이 타당합니다. 즉, world space의 축은 돌지 않았지만 object space의 축은 돌아갔다고 보는 겁니다.

이런 상황에서 우리는 어떤 회전이 가해졌는지를 찾아낼 수 있습니다.

Inverses of Translation and scaling

회전, 확대, 이동을 했다면 다시 반대로 가는 작업도 존재할 수 있습니다. 조립은 해체의 역순입니다. 이들은 약간 다릅니다. Inverse translation은 어렵지 않습니다. 이동한 만큼 되돌아오면 그만입니다. Scaling역시 배수 만큼 역수를 취하면 그만입니다.

Inverse Rotation

inverse translation, inverse scaling은 각각 traslation transform과 scaling transform과 곱하면 identity matrix를 얻었습니다. Rotation도 크게 다르지 않을 것이라고 예상할 수 있을 것 같습니다. 왜냐하면, Identity matrix가 나왔다는 것은 한 행렬이 다른 행렬의 역행렬이며 현재 공간 상에서 정반대의 행동을 암시하기 때문입니다.