[ Open Data Structures ] Red-Black Trees - 3

2-4 Tree와 Red-Black Tree(이하 RBT)가 명백한 관계가 있음을 보였습니다. 추가로 Add/Remove Operation을 RBT에서도 효과적으로 수행할 수 있다는 사실도 확인했습니다. 이미, Binary Search Tree에서 새로운 Leaf node를 추가함으로써 Add operation을 구현할 수 있다는 점은 알고 있습니다. 따라서 2-4 Tree에서 보았던 5개의 Children node를 분할하는 Split method를 RBT에 적용하는 것이 핵심이 될 것입니다. 5개의 Children node를 가진 node는 RBT에서는 하나의 Black node를 가진 Red node와 red node하나, 총 두 개의 Red node를 Children node로 가지는 Black node에 대응하여 나타납니다. 이 경우엔 두 개의 Children node를 Black으로 만들고 Parent node였던 Black node를 Red node로 바꾸면서 Split을 수행할 수 있습니다.

Add operation에서 2-4 Tree의 성질을 활용했던 것처럼 Remove Operation에서도 2-4 Tree가 Sibling의 Child node를 끌어온다거나 두 Node를 병합하는 방법을 활용합니다. Merge는 Split과 정반대의 역할을 하며 두 개의 Black node를 red로 바꾸며 해당 red의 parent는 black으로 변환하는 과정을 포함합니다. Sibling의 child node를 끌어오는 과정은 상당히 복잡하며 Rotation과 Recolouring 과정이 필요합니다.

주의해야 할 점은 앞서 살펴보았던 것처럼 2-4 Tree는 Degree property에 근거하여 4개를 초과하는 Node를 Child로써 가질 수 없는데, 5개의 Children node를 가졌다는 것은 4개의 children을 가진 node에 Add 작업을 통해 어떤 node u를 추가한 상황입니다. RBT에서 이에 상응하는 상황은 Black node가 두 개의 Red node(그 중 하나는 Red node를 child node로써 포함하고 있다)를 가진 상황에서 또 node를 추가한 상황입니다. Figure a1.2.3는 Addition operation 중 발생하는 Split의 일례를 보여주고 있습니다.

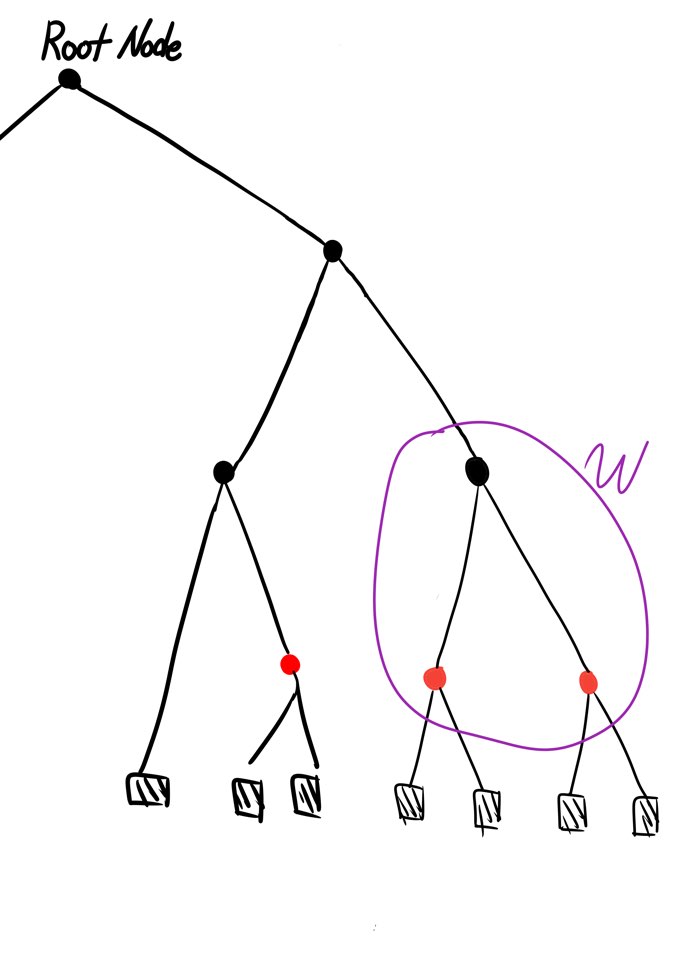
Figure a.1

 

Figure a.2

Figure a.3

전 글에서 작성했던 것처럼 보라색영역은 2-4 Tree와 정확히 대응하는 Node를 나타냅니다. 

Left-Leaning Red-Black Trees

사실, RBT를 단 한 줄로 정리할 수 있는 정의는 존재하지 않습니다. 다만, RBT는 어떤 구조로서 존재하며 전에 언급했던 두 가지 Properties(Black-Height, No-Red-Egde)를 유지시키는 다양한 방법들이 존재할 뿐입니다. 서로 다른 구조를 가지는 RBT는 이 두 가지 Properties를 유지하는 각각의 방법이 있으며 여기서는 두 가지의 Properties에 추가로 다음과 같은 Property를 만족하는 RBT를 구성하기로 합니다.

Additional Property

RBT내부의 모든 임의의 node u에 대해서 u.left가 Black이라면 u.right 역시 black입니다. (Left-Leaning)

Left-Leaning에 따르면 사실 Red-Black Tree - 2에 등장한 Figure a는 Root node의 우측 node가 이 Property를 위반하는 Tree가 됩니다. 구태여 이런 Property를 도입한 이유는 Add/Remove operation 수행 시 Tree를 업데이트 하는 과정에서 발생하는 계산의 양 자체를 줄여줄 수 있기 때문입니다(마주치는 논리적 판단상황을 현격하게 줄일 수 있다는 뜻입니다.). 2-4 Tree의 맥락에서 보면 Degree에 따라서 RBT에 대응하는 다음과 같은 각각의 성질이 있음을 암시합니다.

2 Degree node : 두 개의 black node를 갖는 black node. 

3 Degree node : 좌측에 Red, 우측에 black node를 갖는 black node.

4 Degree node : 두 개의 red node를 갖는 black node.

본격적으로 Add operation을 구현하기 전에 Figure b.1과 Figure b.2에 보이는 Colour에 관한 몇 가지 간단한 Subroutines를 만들고 시작하는 편이 좋습니다. 

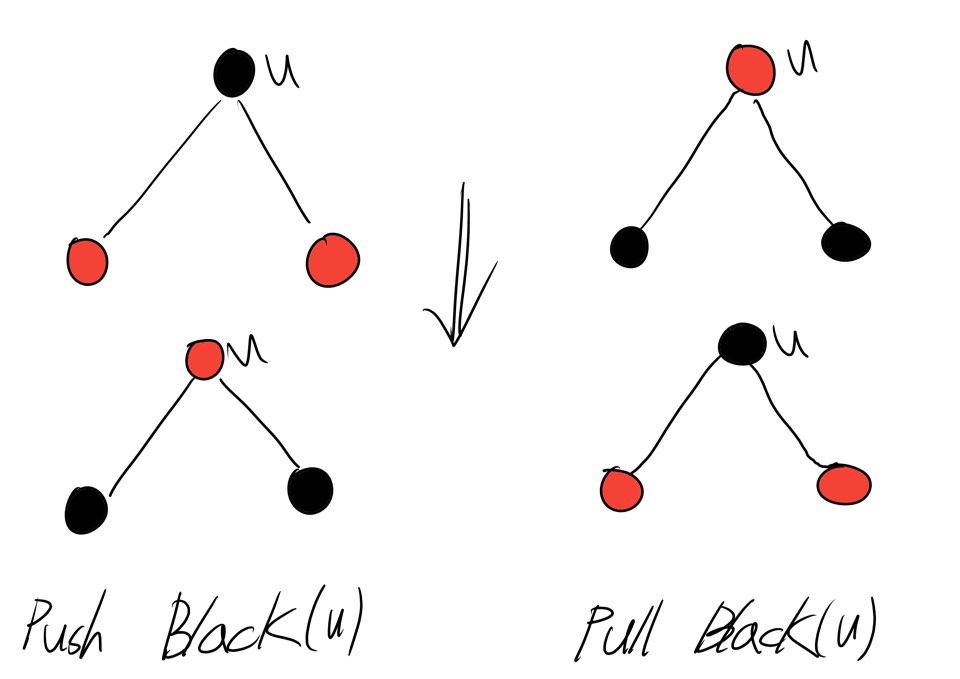
Figure b.1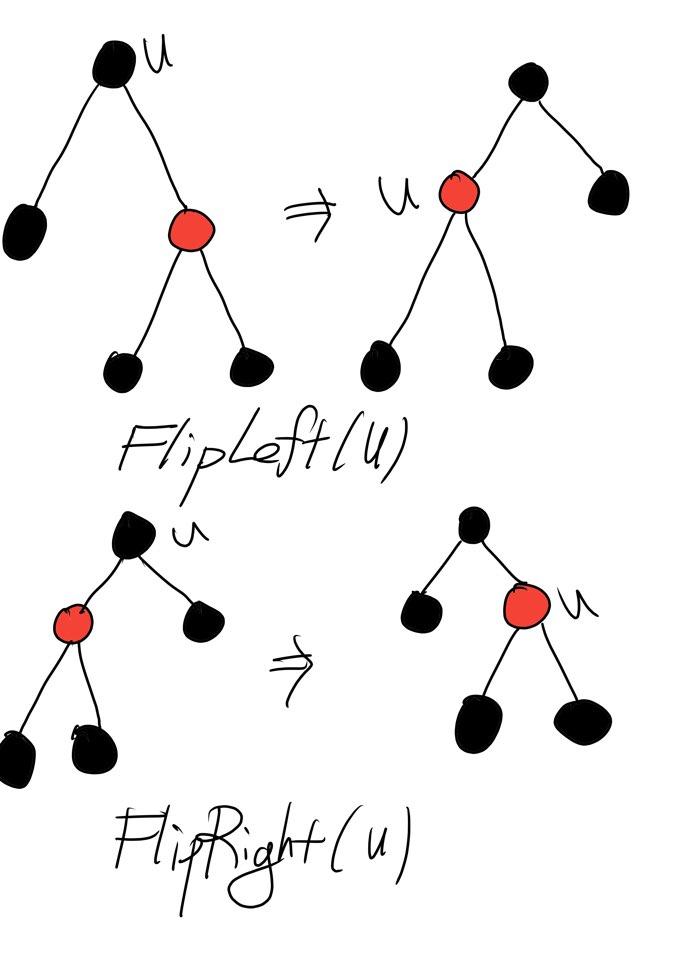

Figure b.2

Figure b.1는 Black Height Property를 유지하며 색깔을 조정합니다. PushBlack(u)는 두 개의 Red Node를 가진 Black node를 Parameter로 node u를 취합니다. 받은 black node u를 Red로, u가 가진 Red Children을 Black으로 칠합니다. PullBlack(u)는 PushBlack(u)의 정반대의 기능을 수행합니다. SwapColours라는 추가적인 함수를 만들어 두 개의 서로 다른 node의 색을 바꿔주는 간단한 함수를 구현해야 합니다.

Figure c

Figure d

 

Figure e

Figure f

상당히 직관적으로 작성된 FlipLeft의 경우엔 u와 u.right의 색을 서로 바꾸고 Treap에서 소개된 Rotation을 통해 좌측으로 회전시킵니다. 따라서 이 함수는 두 node의 색을 바꿀 뿐만이 아니라 Child-Parent의 관계까지 바꾸게 된다는 뜻입니다. 특히, FlipLeft는 Left-Leaning property를 위반하는 node u를 복구하는데 상당히 유용하게 작용합니다. 따라서 이 함수가 수행된특별한 경우에 한해서는 Black-Height, No-Red-Edge의 성질을 위반할 수 없다는 사실을 확인할 수 있습니다. FlipRight는 FlipLeft의 대칭적인 함수의 역할을 수행하기 때문에 특별히 살펴볼 만한 것은 없습니다.