[ Open Data Structures ] - ScapeGoat - 1

 Treap은 Node에 Priority를 통해 Heap성질을 활용하여 Tree의 Balancing을 노렸습니다. 이번엔 ScapeGoat라는 방법을 통해 Tree의 Balancing을 유도해보도록 합시다. ScapeGoat는 Partial-Rebuilding Operation을 통해 Balancing을 꾀합니다. 이 Operation이 수행되는 동안, SubTree는 완전히 분해됐다가 가장 Balanced 형태로 재결합하게 됩니다.

The capegoat라는 말은 뭔가 일이 잘못되었을 때, 인간이 가장 먼저 하는 행동 중 하나가 책임을 물릴 대상을 물색하고 책임자가 선정되면 그 사람이 남은 일을 알아서 처리하도록 한다는 점에서 착안한 단어입니다. 어떤 점이 이런 성질과 닮았는지 확인하도록 해봅시다.

어떤 Root의 Subtree를 분해했다가 재결합하는 다양한 방법이 존재하지만 다음과 같은 방법이 가장 심플하다고 알려져 있습니다. 어떤 Root node u로부터 Tree를 Traverse하며 순서대로 Array a에 node를 모두 모읍니다. 다음, 정수 n을 node의 개수로 표현한다면 Array a를 통해 재구성한 Tree의 Root를 a[m] (이때, m = a.length / 2)로 두고 Left subtree에 a[m > elements]를, Right subtree에 a[m < elements] 각각 재귀적인 방법을 동원하여 달아줍니다.

Rebuild라는 함수는 어떤 node를 받고 해당 노드의 Subtree를 분해-결합합니다. 노드는 포인터이기 때문에 포인터들의 배열인 Pointer to Pointer가 사용되는 모습을 볼 수 있습니다. 추가적으로 두 개의 함수를 구현하는 것이 편한데 하나는 Tree를 하나의 배열로 모아주는 역할을 하는 PackIntoArray함수이고 다른 하나는 반대로 결합하는 BuildBalance함수입니다.

보시면 입력을 받은 노드의 Subtree들을 순회하며 분해하여 배열로 모아주는 모습을 확인할 수 있습니다. BuildBalanced함수는 반환값이 존재하는데 새롭게 결합한 Tree의 Root를 반환해줍니다.

GetSizeOfNode는 Parameter로 전달받은 Node가 가진 Node의 개수를 반환하는 Function입니다. 이 Rebuild Function을 호출할 때 필요한 Running time은 O(GetSizeOfNode(u))와 같습니다. 이 Rebuild Function이 호출된 이후의 n개의 node를 가지는 트리 중 이 Tree보다 낮은 높이를 가질 수는 없습니다. 다음은 PackIntoArray함수입니다. 재귀를 통해 구현했기 때문에 이해하기가 번거롭고 짜증납니다. 재귀함수, Dynamic Programming만 보면 주체할 수 없는 분노가 느껴집니다.

ScapeGoat는 현재 Tree가 포함한 node의 개수를 가리키는 n과 Tree가 가졌던 최대 Node의 개수를 가리키는 q를 사용합니다.  즉, Add Operation을 진행하며 가졌던 가장 많은 Node를 q에 저장해두는 것입니다. 이를 어디에 활용하는지는 차차 설명이 됩니다.

n(현재 node의 개수)과 q(기록된 최대 node의 개수)는 첫 번째 부등식을 항상 만족하며, 이 ScapeGoat로 balancing을 유도하는 Tree에선 높이가 다음과 같은 n과 q의 부등식을 반드시 만족합니다.

Addition

Search Operation은 Binary Search Tree에서의 Operation과 다를 바가 없습니다. Addition Operation 역시, 마지막 node를 찾아 그곳에 달아준다는 점에선 큰 상관이 없습니다. 만약, 추가된 Node u의 깊이[Depth]가 log_{3/2}(q)를 초과하지 않는다면 별다른 조치를 취하지 않고 두더라도 충분히 Balanced 상태일 가능성이 높습니다. 하지만 다음과 같은 경우라면 ScapeGoat를 찾아서 Tree를 Rebuild를 통해서 높이를 낮춰야 할 필요가 있습니다. 따라서, Tree에 node가 추가될 때마다 node의 개수를 추적하는 n과 q를 올려주며 Rebuild가 실행되어야 할 상황을 판단할 수 있어야 합니다.

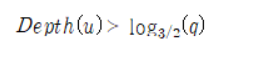
Figure 1

이런 상황을 마주했을 땐, node u에서 시작해 Root node r을 향해 거슬러 올라가며 ScapeGoat가 될 node를 찾아서 ScapeGoat node의 Subtree를 Rebuild합니다. Rebuild라고 함은 ScapeGoat로 선정된 node부터 시작해서 Tree를 완전히 해체한 뒤 다시 결합한다는 뜻입니다. log_{3/2}(q)와 ScapeGoat의 연관성에 대한 증명은 뒤로 미루도록 하겠습니다.

Figure 2

ScapeGoat인 node w는 위와 Figure 1을 만족하는 상당히 불균형한 Tree를 가지고 있습니다. w.child는 w의 subtree를 이르며 size(w)는 parameter의 node w가 갖고 있는 subtree 내의 node 개수를 이르는 말입니다. 그럼 w의 어떤 자식 노드는 w의 전체 노드의 2/3가 한쪽에 몰아져있다는 뜻으로 Addition Operation을 수행하기 전에도 ScapeGoat는 완전히 균형이 맞춰진 Tree가 아니었을 겁니다(Figure 1에 따라 Figure 2의 Property를 갖기 때문입니다.). 따라서, node w를 Rebuild하게 되면 Height가 최소한 1이 떨어지고 ScapeGoatTree의 전체 높이[height]는 log_{3/2}(q)보다 작아지게 될 것입니다.

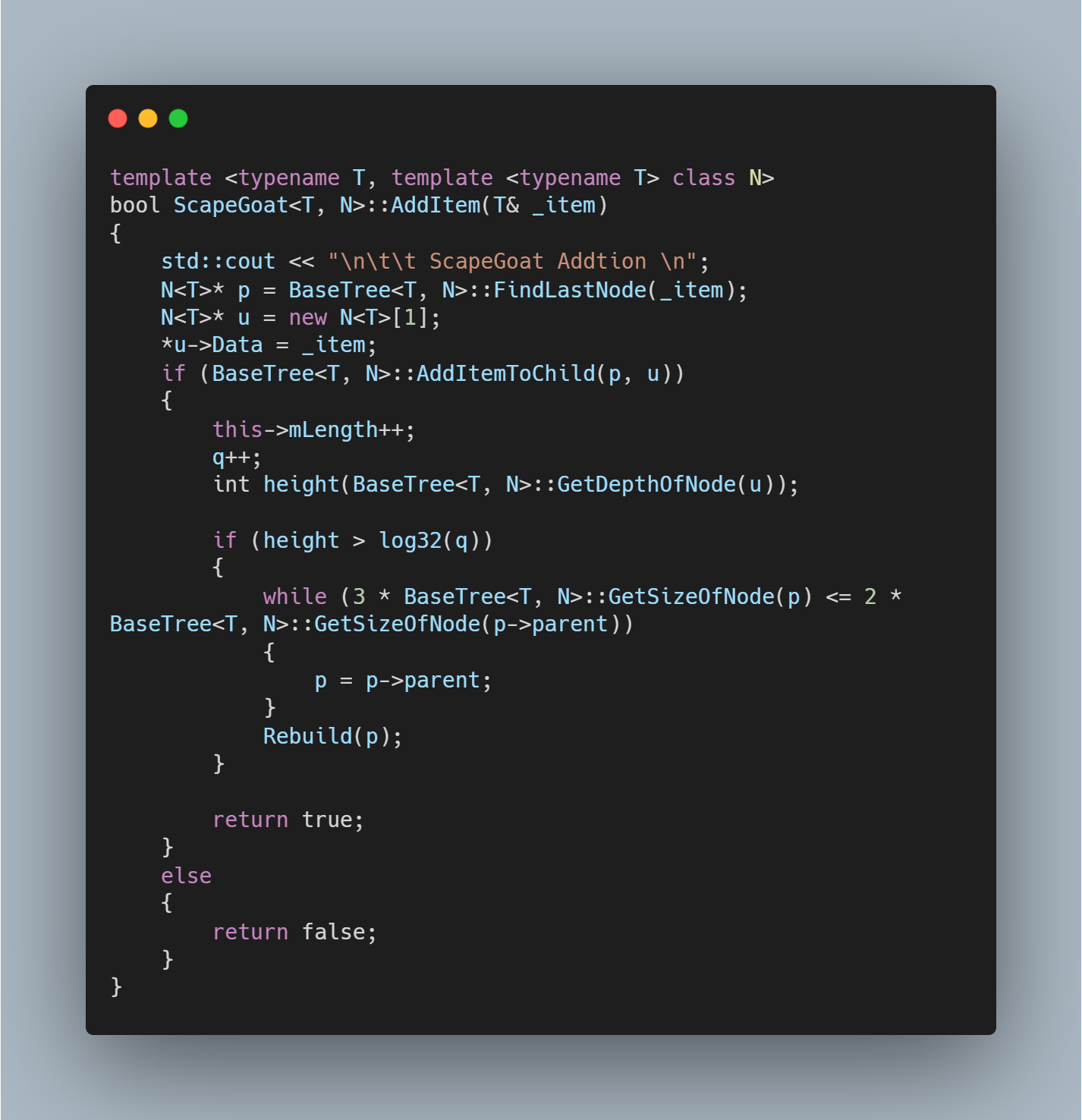
Rebuild가 필요한 상황과 방법을 코드로 그대로 구현했습니다. PackIntoArray 함수의 재귀부분이 까다로웠을 뿐이지 코드 자체가 난해한 것은 전혀 아닙니다. 이 코드의 신뢰성을 뒷받침하는 정교한 논리가 이해하기 상당히 어려웠습니다. 만일, ScapeGoat를 찾는 시간과 그 Subtree를 Rebuild하는 시간을 제외한다면 Addition Operation의 Running time은 Figure 3를 만족하며 w를 찾는 시간과 정확히 같습니다. 

Remove Operation

삭제는 Unbalanced Binary Search Tree에서 삭제동작과 상당히 유사합니다. 이 삭제동작이 실질적으로는 Tree 내부의 임의의 node의 Height를 증가시키지 않는다는 점에 주목해야 합니다. Node를 삭제한 뒤, n(현재 구현한 코드에선 mLength와 완전히 같습니다.)를 1 감소시키고 q는 그대로 둡니다. 마지막으로 q >2n을 검증해보고 참이라면 Root node부터 시작해서 완전히 Rebuild 한 후에 q를 n과 같은 값으로 두면 됩니다. 마찬가지로 Running time은 Tree자체의 높이에 비례하며 O(log(N))입니다. 

참고자료 :

ScapeGoat Tree | Set 1 (Introduction and Insertion) - GeeksforGeeks

ScapeGoat Tree | Set 1 (Introduction and Insertion) - GeeksforGeeks